자료구조
- 자료 사이의 논리적 관계를 컴퓨터나 프로그램에 적용하기 위해서는 자료의 추상화가 필요함
→ 자료구조(data structure): 추상화를 통해 자료의 논리적 관계를 구조화한 것 - 자료가 복잡해지거나 소프트웨어가 복잡해질수록 자료구조의 중요성이 강조됨
- 추상화: 공통적인 개념을 이용하여 같은 종류의 다양한 객체를 정의하는 것
- 자료(데이터)의 추상화: 다양한 객체를 컴퓨터에서 표현하고 활용하기 위해 필요한 데이터의 구조에 대해서 공통의 특징만을 뽑아 정의한 것
- 자료의 추상화와 구조화가 적절히 이루어지지 못하면 소프트웨어는 비효율적으로 개발되거나 비효율적으로 수행되거나 소프트웨어의 확장성에 문제가 생기거나 소프트웨어의 유지보수에 문제가 생기거나 할 수 있음
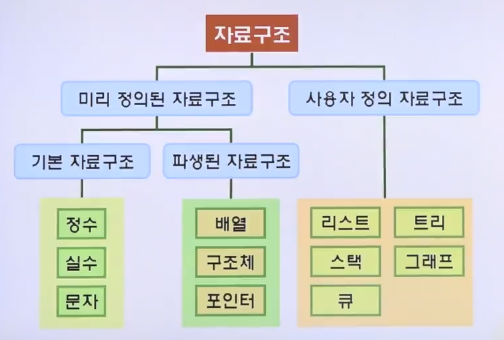
- 미리 정의된 자료구조
- 프로그래밍 언어에서 제공함
- 프로그래밍 언어 설계나 컴파일러 구현 단계에서 정의되어 개발자에게 제공되는 자료구조
- 사용자 정의 자료구조
- 개발자가 정의하여 사용함
- 소프트웨어 개발 중에 개발자에 의해 만들어지는 자료구조(리스트, 스택, 큐, 리스트, 그래프 등)
배열
동일한 자료형을 갖는 여러 개의 데이터를 동일한 변수 이름의 방에 일렬로 저장하는 자료 집합체 (원소+인덱스)
- 원소(요소): 자료 집합체에서 각 원소의 항목값 → 데이터
- 인덱스(첨자): 자료 집합체에서 각 원소가 저장된 방을 접근하기 위한 방 번호에 해당하는 것 → 번호
1차원 배열
- 가장 간단한 형태의 배열
- 한 개의 인덱스(첨자)를 사용해서 원소에 직접 접근함
- 배열의 원소들은 컴퓨터 메모리의 연속적인 기억장소에 할당되어 순차적으로 저장됨
- 배열 A의 크기를 k라고 가정하고 시작 주소를 a라고 가정하면, A[i]의 저장 주소는 a+i*k가 됨
다차원 배열
- 2차원 배열의 저장 순서
- 열 우선 순서 저장: 첫 열에 있는 각 행의 원소를 차례대로 컴퓨터 메모리에 저장하고 다음 열로 이동하여 각 행에 있는 원소를 차례대로 컴퓨터 메모리에 저장하는 방법
- 행 우선 순서 저장: 첫 행에 있는 각 열의 원소를 차례대로 컴퓨터 메모리에 저장하고 다음 행으로 이동하여 각 열에 있는 원소부터 차례대로 컴퓨터 메모리에 저장하는 방법
- n차원 배열
희소 행렬
- 원소 값이 0인 원소가 그렇지 않은 원소보다 상대적으로 많은 행렬
- 0의 값을 저장하기 위해 컴퓨터 메모리의 낭비를 막고, 처리의 효율성을 높이기 위해 사용됨
- 희소 행렬의 0인 원소는 저장하지 않고, 0이 아닌 값 만을 따로 모아서 저장하는 방법
- 0이 아닌 각 원소를 (행 번호, 열 번호, 원소 값)의 형태로 나타내면, 2차원 배열로 표현 가능함
리스트
- 순서 리스트(ordered list)라고도 함
- 1개 이상의 원소들이 순서를 가지고 구엇됨
- A = (a_1, a_2, … a_i, a_n) 과 같이 표시하며, a_i는 i번째 원소를 나타내고, a_n의 n은 리스트의 크기가 됨
선형 리스트의 구현(배열을 통한 구현)
- 선형 리스트와 1차원 배열은 순차적인 구조를 가지고 있으므로 1차원 배열로 간단하게 표현할 수 있음
- 원소를 삽입하기 위해서는 삽입될 위치 이후의 원소들의 순서를 그대로 유지하면서 원소를 삽입해야 함
→ 삽입할 위치에 있는 원소와 그 다음의 원소들을 모두 한 칸씩 뒤로 이동시켜야 함 - 원소 삭제의 경우에도 삭제할 원소를 찾아 삭제한 후, 그 뒤에 있는 모든 원소들을 한 칸씩 앞으로 이동시켜야 함
선형 리스트의 구현(연결 리스트(linked list))
- 노드 간의 포인터 연결을 통해서 구현됨
- 각 노드는 적어도 두 종류의 필드, 원소 값을 저장하는 데이터 필드와 노드 연결을 위한 링크 필드를 가짐
- 선형 리스트의 논리적 순서만을 지원함
- 연결 리스트의 종류
- 단일 연결 리스트
- 특정 노드의 링크 필드를 사용해서 후행 노드를 가리킴
- 특정 노드의 후행 노드는 쉽게 접근할 수 있지만, 선행 노드에 대한 접근은 헤드 노드부터 새로 시작해야 함
- 이중 연결 리스트
- 특정 노드의 첫번째 링크는 후행 노드를 가리키고 두번째 링크는 선행 노드를 가리킴
- 특정 노드에서 후행 노드 뿐만 아니라 선행 노드에 대한 접근을 쉽게 제공하기 위한 것
- 단일 연결 리스트
스택과 큐
스택
- 데이터의 삽입과 삭제가 한쪽 끝에서만 이루어지는 자료구조
- 가장 먼저 입력된 데이터가 가장 나중에 제거되는 선입후출(FILO, First-In-Last-Out) 특징을 가짐
- 스택 오버플로(overflow)
- 삽입 연산을 수행할 때 발생함
- 스택을 위해 할당된 저장 공간을 초과해서 더 이상 데이터를 삽입할 수 없는 현상
- 스택 언더플로(underflow)
- 삭제 연산을 수행할 때 발생함
- 스택에 데이터가 존재하지 않으면 삭제가 일어나지 않는 현상
큐
- 선형 리스트의 한쪽 끝에서는 데이터의 삭제만 이루어지고, 다른 한쪽 끝에서는 데이터의 삽입만 이루어지는 자료구조
- 가장 먼저 입력된 데이터가 가장 먼저 제거되는 선입선출(FIFO, First-In-First-Out) 특징을 가짐
- 오버플로(overflow), 만원 상태
- 삽입 연산을 수행할 때 발생함
- 큐를 위해 할당된 저장 공간을 초과해서 더 이상 데이터를 삽입할 수 없는 현상
- 하지만 이 경우 반드시 큐에 n개의 항목이 가득 차 있다는 것을 의미하는 것은 아님
- 큐가 가득 채워진 상태를 결정하기 위한 다른 방법이 필요
- 언더플로(underflow)
- 삭제 연산을 수행할 때 발생함
- 큐에 데이터가 존재하지 않으면 삭제가 일어나지 않는 현상
트리
- 데이터 간의 관계를 나타내는 비선형 자료구조
- 노드라고 불리는 부분과 노드를 연결하는 가지로 구분됨
- 노드 사이에는 계층적인 관계성을 갖음
용어 정리
- 노드(node): 정보 항목
- 루트(root): 빈 트리가 아닌 경우에 맨 꼭대기에 있는 하나의 노드
- 차수(degree): 각 노드에 있는 가지의 수
- 잎 노드(leaf node), 단말 노드(terminal node): 노드의 차수가 0인 노드
- 내부 노드(internal node), 비단말 노드(non-terminal node): 루트 노드와 단말 노드를 제외한 나머지 노드
- 조상 노드: 루트 노드로부터 어떤 노드 X까지의 경로(가지들의 모음) 상에 존재하는 모든 노드를 X의 조상 노드라고 함
- 자손 노드: 어떤 노드 X에서 단말 노드까지의 경로 상에 존재하는 모든 노드를 자손 노드라고 함
- 레벨(level): 루트 노드로부터의 거리(가지의 수)를 의미함
- 트리의 깊이: 루트 노드로부터 가장 긴 경로에 있는 단말 노드의 레벨에 1의 값을 더한 것
- 서브 트리(subtree): 특정 노드를 루트 노드로 하고, 그 아래에 있는 연결된 구조의 트리
- 숲(forest): n개의 서브 트리를 가진 트리에서 루트 노드를 제거해서 얻을 수 있는 분리된 서브 트리의 집합
이진 트리
- 트리 중에서 차수가 2인 트리
- 모든 노드의 차수는 최대 2를 넘지 않음
- 모든 노드는 최대 2개의 서브 트리를 가짐
- 각 서버 트리는 왼쪽 서브 트리와 오른쪽 서브 트리로 구분됨
- 왼쪽 노드와 오른쪽 노드에 ‘순서’의 의미를 부여함
- 이진 트리의 각 서브 트리는 다시 이진 트리가 됨
- 이진 트리의 높이
- N개의 노드를 가진 이진 트리의 높이를 계산으로 구할 수 있음
- 최대 높이: N으로 노드의 개수와 같음
- 최소 높이: 최대 2개의 자식 노드를 갖는 경우로서 [log_2 N] + 1이 높이가 됨
- 이진 트리 순회 연산: 일정한 순서에 따라 트리에 있는 각 노드를 한 번씩 방문하는 것
- DLR(전위 순회; preorder): 루트 노드 방문 → 왼쪽 서브 트리 방문 → 오른쪽 서브 트리 방문
- LDR(중위 순회; inorder): 왼쪽 서브 트리 방문 → 루트 노드 방문 → 오른쪽 서브 트리 방문
- LRD(후위 순회; postorder): 왼쪽 서브 트리 방문 → 오른쪽 서브트리 방문 → 루트 노드 방문
- 포화 이진 트리
- 깊이가 k인 이진 트리 중에서 노드의 개수가 2^k-1개인 이진 트리
- 깊이가 k인 이진 트리가 가질 수 있는 노드의 최대 개수는 (2^k-1)-1개
- 단말 노드의 개수가 (2^k-1)-1개
- 각 레벨에서 빈자리가 없이 노드를 모두 가지고 있음
- 모든 내부 노드들은 2개의 자식 노드를 가짐
- 완전 이진 트리
- 트리의 최대 레벨이 k일 때, 레벨 k-1까지는 포화 이진 트리를 형성하고, 레벨 k에서는 왼쪽부터 오른쪽으로 채워진 트리임
- 총 노드의 개수가 (2^k+1)-1을 초과하지 않으면서, 포화 이진 트리의 노드 번호에 해당하는 연속적인 번호를 갖는 트리임
- 경사 이진 트리: 한 쪽 방향으로만 가지가 뻗어 나간 이진 트리
그래프
- 정점(vertex)들의 유한 집합 V와 두 개의 정점을 연결하는 간선(edge)들의 유한 집합 E로 정의
- G = (V, E)로 표시됨
- 두 정점이 간선으로 직접 연결되어 있으면 두 정점은 인접(정점 간의 관계)해 있다고 하며, 해당 간선은 두 정점에 부수되었다(정점과 간선 간의 관계)고 함
- 경로: 간선으로 연결된 정점들의 순차적 나열을 의미함
- 경로의 길이: 경로에 포함된 간선의 개수
- 단순 경로: 경로 상에 존재하는 정점들이 모두 다른 경로
- 사이클: 세 개 이상의 정점을 가진 경로 중에서 시작 정점과 끝 정점이 같은 경로
- 단순 사이클: 시작 정점과 끝 정점을 제외하고 모든 정점이 다른 사이클
그래프의 종류

- 무방향 그래프: 간선이 방향이 없는 간선으로 연결된 그래프
- 서로 다른 모든 저점들 사이에 경로가 존재한다면 그래프가 서로 연결되었다고 함
- 한 정점의 차수: 정점에 부수된 간선의 개수
- 방향 그래프: 두 정점을 연결하는 간선이 방향성을 가지는 간선으로 연결된 그래프
- 진입 차수(indegree): 다른 정점에서 해당 정점을 향하는 간선의 개수
- 진출 차수(outdgree): 해당 정점으로부터 다른 정점으로 향하는 간선의 개수
- 트리는 그래프의 특수한 형태로 보며, 무방향 그래프에서 모든 정점이 서로 연결되어 있으면서 사이클이 존재하지 않음
그래프의 표현
- 인접 행렬: n개의 정점을 가진 그래프를 표현하기 위해서는 n*n 크기의 2차원 배열을 이용함
- 인접 리스트
그래프의 탐색
- 그래프의 모든 정점을 체계적으로 방문하는 것
- 깊이 우선 탐색(DFS): 최근의 방문하지 않은 인접한 하나의 정점을 우선적으로 방문함
- 너비 우선 탐색(BFS): 최근의 방문하지 않은 인접한 모든 정점을 모두 방문함
'CS' 카테고리의 다른 글
| [프로그래밍 언어론] 구문론과 의미론 (1) | 2023.11.22 |
|---|---|
| [프로그래밍 언어론] 프로그래밍 언어 패러다임 (1) | 2023.11.22 |
| [프로그래밍 언어론] 프로그래밍 언어의 발전 및 동작원리 (0) | 2023.11.22 |
| [프로그래밍 언어론] 프로그래밍 언어 소개 (1) | 2023.11.22 |
| [컴퓨터과학개론] 컴퓨터와 데이터 (0) | 2023.11.19 |
![[컴퓨터과학개론] 자료구조](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FxT2pL%2FbtsAEoKGuu7%2FAAAAAAAAAAAAAAAAAAAAAMliI_Qq0QO7KmpKb2iPgfmmr2yyYiihKBykFdIlmk6w%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DGyXCs4cdGJmbJfY9ht552CAmzUo%253D)