원소 간 다대다 관계를 가지는 구조로 계층적 구조나 망형 구조를 표현하기에 적절합니다.

그래프
그래프는 정점과 정점 사이를 연결하는 간선으로 이루어진 비선형 자료구조 입니다. 정점(Node) 집합과 간선(Edge) 집합으로 표현할 수 있습니다.
그래프는 우리가 흔히 쓰는 지하철 경로 탐색 등에도 사용되는 소프트웨어 개발에서 중요한 자료구조 중 하나입니다. 정점은 여러 개의 간선을 가질 수 있으며, 크게 방향이 존재하는 방향 그래프와 방향이 존재하지 않는 무방향 그래프로 나눌 수 있습니다. 간선은 가중치를 가질 수 있으며, 탐색 시 그래프의 정점과 간선의 집합에서 계속 순환 가능한 사이클이 있습니다. 때문에 탐색 시 무한루프에 빠지지 않도록 사이클을 잘 찾아줄 필요가 있습니다.
그래프의 종류
- 무방향 그래프: 간선에 방향이 존재하지 않기 때문에 간선으로 이어진 정점끼리는 양방향 이동이 가능합니다. 따라서 (A,B)와 (B,A)는 같은 간선으로 취급됩니다.
- 방향 그래프: 간선에 방향이 존재하는 그래프입니다. 양방향으로 갈 수 있더라도 <A,B>와 <B,A>는 다른 간선으로 취급됩니다.
- 연결 그래프: 모든 정점이 서로 이동 가능한 상태인 그래프입니다. 특정 정점에서 또 다른 정점까지 모든 경우의 수에서 이동 가능해야 합니다.
- 비연결 그래프: 특정 정점에서 간선이 존재하지 않는 그래프입니다.
- 완전 그래프: 모든 정점끼리 연결된 상태인 그래프를 말합니다. 따라서, 한 정점의 간선의 수는 모든 정점의 수 -1이 됩니다. 또한 모든 정점의 수 -1 * 모든 정점의 수를 곱하면 모든 간선의 수를 알 수 있습니다.
그래프의 구현
인접 행렬(이차원 배열로 구현)
정점의 크기만큼 이차원 배열을 만들고 연결이 되지 않은 상태로 초기화합니다. 그리고, 행렬의 열부분을 시작정점, 행부분을 도착 정점으로 두고 true값을 넣어주면 간선이 연결된 것으로 간주합니다. 만약 간선에 가중치를 넣고 싶다면 null 혹은 임의의 가중치를 넣어주시면 됩니다. 참고로 무방향 그래프는 모든 값을 대칭으로 넣어주시면 됩니다.
const graph = Array.from(Array(5), ()=>Array(5).fill(false));
graph[0][1] = true; // 0 -> 1
graph[0][3] = true; // 0 -> 3
graph[1][2] = true; // 1 -> 2
graph[2][0] = true; // 2 -> 0
graph[2][4] = true; // 2 -> 4
graph[3][2] = true; // 3 -> 2
graph[4][0] = true; // 4 -> 0
인접 리스트(연결 리스트로 구현)
정점의 수만큼 배열을 만들어주고 연결할 정점을 배열에 추가하면 됩니다.
const graph = Array.from(Array(5), () => []);
graph[0].push(1); // 0 -> 1
graph[0].push(3); // 0 -> 3
graph[1].push(2); // 1 -> 2
graph[2].push(0); // 2 -> 0
graph[2].push(4); // 2 -> 4
graph[3].push(2); // 3 -> 2
graph[4].push(0); // 4 -> 0
트리
트리는 몇 가지 제약이 있는 방향 그래프의 일종으로 하나의 정점에서 하위로 뻗어나가는 구조를 가지고 있으며, 가장 상위에 있는 정점을 Root라고 합니다. 각 정점은 Node라고 부르며 더 이상 자식이 없는 노드를 Leef Node라고 합니다. 가리키는 그리고 트리에는 Level이라는 개념이 존재합니다. level은 root로부터 몇 번째 깊이인지를 표현할 때 사용합니다. 그리고 한 정점에서 뻗어나가는 간선을 degree 혹은 차수라고 부릅니다.
트리에서 Root 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가지게 되기 때문에, 정점이 N개인 트리는 반드시 N-1개의 간선을 가지게 되며, 루트에서 특정 정점으로 가는 경로는 반드시 하나만 존재합니다.
트리 구현 시에는 몇 가지 규칙만 지키면 됩니다.
트리(이진트리)의 종류
이진 트리는 탐색을 위한 알고리즘에서 많이 사용하기 때문에 특징을 알아두면 좋습니다. 이진 트리란 정점이 자식을 최대 2개 이상 가지는 트리를 말합니다.
- 완전 이진트리: 마지막 레벨을 제외하고 정점이 채워져있는 트리를 말합니다.
- 포화 이진트리: 마지막 레벨의 정점까지 모두 채워져 있는 트리를 마합니다.
- 편향 트리: 한 방향으로만 정점이 이어지는 것을 뜻합니다.
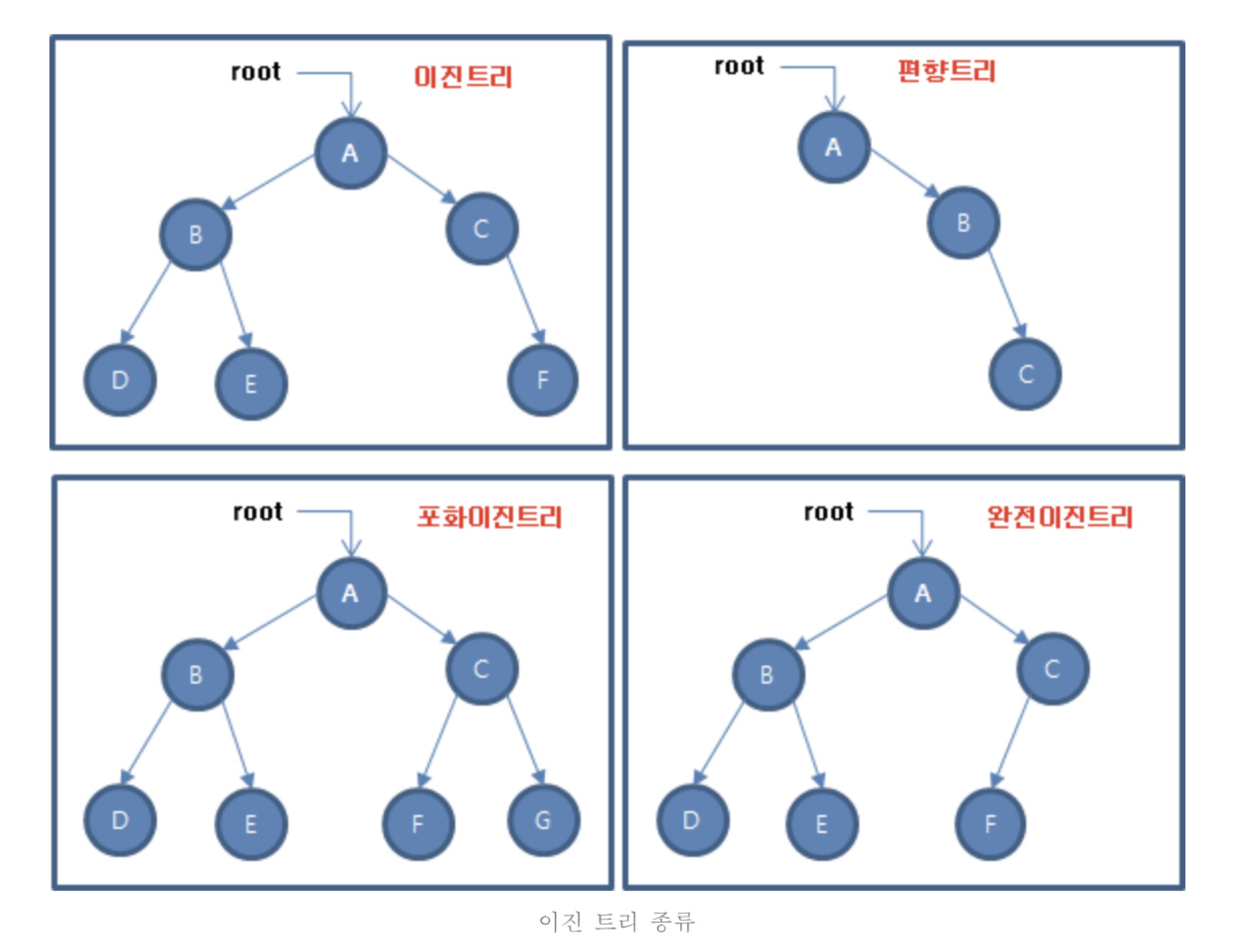
정점이 N개인 이진 트리는 최악의 경우 O(n)이 될 수 있으며, 정점이 N개인 포화 또는 완전 이진 트리는 레벨이 증가됨에 따라 2배씩 정점이 생기기 때문에 시간복잡도는 log N입니다. 높이가 h인 포화 이진 트리는 2^h-1개의 정점을 가집니다. 일반적으로 이진 트리를 직접적으로 사용하는 경우는 많지 않고, 이진 탐색 트리, 힙, AVL 트리, 레드 블랙 트리 자료구조에 응용되어 사용됩니다.
트리의 구현
일반 트리는 그래프에서 구현하는 방법과 동일합니다. 예외적으로 이진 트리의 경우 자식의 수가 2개 이하로 제한되기 때문에 그래프보다 최적화된 방법으로 구현할 수 있습니다. 1차원 배열 혹은 링크가 두 개 존재하는 연결리스트로 구현 가능합니다.
인접 행렬(배열로 구현)
// 0번 인덱스는 편의를 위해 비워둔다.
// Left = index * 2;
// Right = (index * 2) + 1
// Parent = floor(index/2)
const tree = [
undefined,
// 1
9
// 1*2, 1*2+1
3, 8,
// 2*2, 2*2+1, 3*2, 3*2+1
2, 5, undefined, 7
// 4*2, 4*2+1, 5*2, 5*2+1
undefined, undefined, undefined, 4
];
인접 리스트(연결 리스트로 구현)
class Node{
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class Tree{
constructor(node){
this.root = node;
}
display(){
// Level Order
const queue = new Queue();
queue.enqueue(this.root);
while(queue.size){
const currentNode = queue.dequeue();
console.log(currentNode.value);
if(currentNode.left) queue.enqueue(currentNode.left);
if(currentNode.right) queue.enqueue(currentNode.right);
}
}
}
힙(Heap)
힙에 대해 공부하기 전에 먼저 우선순위 큐에 대해서 알고 있어야 합니다. 우선순위 큐란, 일반적인 큐와는 달리 우선 순위가 높은 요소가 먼저 나가는 큐를 말합니다(우선순위 큐는 자료구조가 아닙니다). 우선순위 큐를 구현하는 방법에는 제한이 없으며 다양하게 존재할 수 있습니다. 그 중 하나가 바로 힙입니다.
힙은 이진 트리 형태를 가지며, 우선순위가 높은 요소가 먼저 나가기 위해 요소가 삽입, 삭제 될 때 바로 정렬되는 특징이 있습니다. 우선순위 큐 문제를 만나면 무조건 힙을 써야한다고 생각하실 수 있지만 그렇지는 않습니다. 만약 매번 배열을 우선 순위에 따라 정렬하는 로직을 구현하셨다면 힙보다는 효율성이 떨어지겠지만, 그것 또한 우선순위 큐를 구현했다고 할 수 있습니다. 힙은 우선순위가 높은 요소를 root로 배치하고 root가 먼저 나가는 특징을 가집니다. 루트가 가장 큰 값이 되는 최대 힙과 루트가 가장 작은 값이 되는 최소 힙이 있습니다. 자바스크립트에서는 이러한 힙을 직접 구현해서 사용해야 합니다.
Heap 요소 추가
요소가 추가될 때는 트리의 가장 마지막에 요소를 추가합니다. 요소가 추가된 후 추가된 요소가 부모보다 우선순위가 높다면 부모 정점과 순서를 바꿉니다. 이 과정을 반복하면 결국 가장 우선순위가 높은 정점이 루트가 됩니다. 그리고 요소는 항상 트리의 마지막에 추가가 되기 때문에 힙은 항상 완전 이진 트리입니다. 완전 이진 트리의 시간복잡도는 log N이기때문에 마찬가지로 힙의 요소 추가 알고리즘 또한 **O(log N)**을 가집니다
// 0번 인덱스는 편의를 위해 비워둔다.
// Left = index * 2;
// Right = (index * 2) + 1
// Parent = floor(index/2)
const heap = [undefined];
// 1. 최대 힙에 45를 추가
heap[1] = 45
// 2. 36을 추가
heap[1*2] = 36
// 3. 54 추가
heap[1*2+1] = 54 // 최대 힙에서 45보다 54가 우선순위가 높으므로 순서를 변경해야한다.
// 4. 45와 54의 정점 바꾸기
heap[Math.floor(3/2)] = 54
heap[3] = 45
// 5. 27을 추가
heap[2*2] = 27
// 6. 63을 추가
heap[2*2+1] = 63 // 최대 힙에서 63이 36보다 우선순위가 높으므로 순서를 변경해야한다.
heap[5] = 36
heap[Math.floor(5/2)] = 63 // 최대 힙에서 63이 54보다 우선순위가 높으므로 순서를 변경해야한다.
// 7. 63과 54 정점 바꾸기
heap[Math.floor(2/2)] = 63
heap[2] = 54
// 8. 최대 힙 완성
console.log(heap) // [ undefined, 63, 54, 45, 27, 36 ]
Heap 요소 삭제
요소 제거는 루트만 가능합니다. 루트가 제거되면 가장 마지막 정점이 루트가 됩니다. 이 때, 추가와는 반대로 루트로부터 정점을 아래로 내려야합니다. 루트 정점의 두 자식 정점을 더 우선순위가 높은 정점과 바꿉니다. 두 자식의 정점이 더 우선순위가 낮을 때까지 반복하면 우선순위가 더 높은 정점이 루트 정점이 될 수 있습니다. 시간복잡도는 log N입니다.
// 0번 인덱스는 편의를 위해 비워둔다.
// Left = index * 2;
// Right = (index * 2) + 1
// Parent = floor(index/2)
const heap = [ undefined, 63, 54, 45, 27, 36 ]
// 1. 루트 제거
// 루트를 제거하고 가장 마지막 정점을 루트로 변경
heap.splice(1, 1, ...heap.splice(heap.length-1, 1)) // [ undefined, 36, 54, 45, 27 ]
// 2. 규칙에 따라 루트인 36과 자식 정점 45, 54를 비교하여 큰 값을 루트로 변경합니다.
heap[1] = 54
heap[1*2] = 36
// 3. 이번에는 자식 정점인 27과 비교 하여 자식의 우선순위가 더 낮기 때문에 삭제를 종료합니다.
Heap의 구현(최대 힙)
class MaxHeap {
constructor() {
this.heap = [null]; // 내부적으로 관리할 배열
}
push(value) {
this.heap.push(value); // 가장 마지막에 요소 추가
let currentIndex = this.heap.length - 1;
let parentIndex = Math.floor(currentIndex / 2);
// 루트가 아니거나 부모가 더 우선 순위가 낮지 않을 때까지 순서 변경
// 최소 합인 경우에는 value와 부모요소 비교 시 부등호만 변경해주면 되겠죠?
while (parentIndex !== 0 && this.heap[parentIndex] < value) {
const temp = this.heap[parentIndex];
this.heap[parentIndex] = value;
this.heap[currentIndex] = temp;
currentIndex = parentIndex;
parentIndex = Math.floor(currentIndex / 2);
}
}
pop() {
if (this.heap.length === 2) return this.heap.pop(); // 루트 정점만 남은 경우
const returnValue = this.heap[1]; // 루트 요소 저장
this.heap[1] = this.heap.pop(); // 루트 요소에 마지막 요소로 대체
let currentIndex = 1;
let leftIndex = 2;
let rightIndex = 3;
while (this.heap[currentIndex] < this.heap[leftIndex] ||
this.heap[currentIndex] < this.heap[rightIndex]) {
if (this.heap[leftIndex] < this.heap[rightIndex]) {
const temp = this.heap[currentIndex];
this.heap[currentIndex] = this.heap[rightIndex];
this.heap[rightIndex] = temp;
currentIndex = rightIndex;
} else {
const temp = this.heap[currentIndex];
this.heap[currentIndex] = this.heap[leftIndex];
this.heap[leftIndex] = temp;
currentIndex = leftIndex;
}
leftIndex = currentIndex * 2;
rightIndex = currentIndex * 2 + 1;
}
return returnValue;
}
}
트라이(Trie)
트라이는 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조입니다. 루트는 비어있으며, 간선은 이전 정점으로 새롭게 추가되는 문자 정보를 가지고 있습니다. 그리고 정점은 이전 정점으로부터 더해진 문자열 정보를 가지고 있습니다.
트라이는 검색어 자동완성 혹은 사전 찾기 등에 응용될 수 있습니다. 문자열을 탐색할 때 단순하게 비교하는 것보다 효율적으로 찾을 수 있으며, L이 문자열의 길이일 때 탐색, 삽입은 **O(L)**만큼 걸립니다. 대신 각 정점이 자식에 대한 링크를 전부 가지고 있기 때문에 저장 공간을 더 많이 사용하게 됩니다. 해시/연결리스트로 구현할 수 있습니다.
class Node{
constructor(value = ""){
this.value = value;
this.children = new Map();
}
}
class Trie{
constructor(){
this.root = new Node(); // 빈 노드 생성
}
// 문자열 추가
insert(string){
let currentNode = this.root; // 탐색을 위해 루트부터 시작
// 문자열을 앞에서부터 하나씩 자르면서 순회
for(const char of string){
if(!currentNode.children.has(char)){ // 만약 없다면 새롭게 추가
currentNode.children.set(
char,
new Node(currentNode.value + char)
);
}
currentNode = currentNode.children.get(char); // 다음 정점으로 이동
}
}
// 문자열 탐색
has(string){
let currentNode = this.root;
for(const char of string){
if(!currentNode.children.has(char)){
return false;
}
currentNode = currentNode.children.get(char);
}
return true;
}
}
완벽한 자료구조는 없습니다. 특정 상황에서 더 유용한 자료구조와 덜 유용한 자료구조만 존재할 뿐입니다. 그렇기 때문에 우리는 다양한 자료구조에 대해서 알고 있어야 하며 상황에 따라 적절한 자료구조를 사용해야 합니다.
'DataScience > Data Structure' 카테고리의 다른 글
| 알고리즘 - 정렬 (0) | 2022.12.19 |
|---|---|
| 알고리즘 - 이진탐색 (0) | 2022.12.19 |
| 알고리즘 - 시간복잡도 (0) | 2022.12.19 |
| 자료 구조의 종류 - 단순 구조와 선형 구조 (1) | 2022.12.09 |
| 자료구조와 알고리즘을 공부해야 하는 이유? 자바스크립트 똑똑하게 쓰기! (0) | 2022.12.06 |
